Surface tension stabilizes planar gas–liquid interfaces by smoothing ripples. It may be surprising, then, that at cylindrical interfaces it causes the liquid to break up. This is called the Plateau–Rayleigh instability. In Fig. P4.12(a) a wettable fiber of radius b is coated with a liquid film of outer radius a, where a is small enough that Bo ≪ 1 and gravity is negligible. In response to small disturbances (e.g., vibrations), such a film ordinarily rearranges into a necklace-like set of droplets, as shown in Fig. P4.12(b).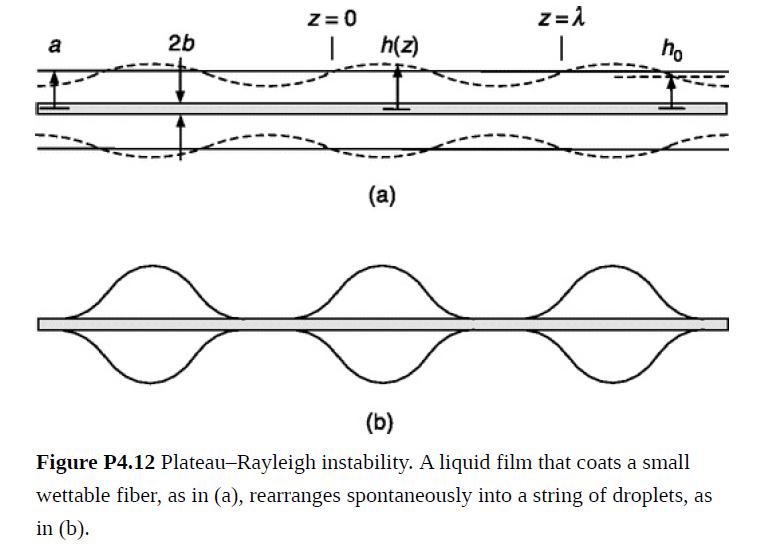

equals that in the surface energy, γΔS. Suppose that something causes a sinusoidal deformation of the interface, as in the dashed curves in Fig. P4.12(a). Such a deformation might have any wavelength λ. What is to be shown is that the area of the wavy surface (S_w) is smaller than that of the smooth one (S₀) whenever λ > 2πa. A practical consequence of this is that a liquid cylinder that is longer than its circumference will break up spontaneously.

(a) The local radius of a slightly wavy cylinder with average radius h₀ is

where ε ≪ 1. [For clarity of labeling, the wave amplitude εh0 in Fig. P4.12(a) is greatly exaggerated.] For the wavy and smooth films to have the same volume, show that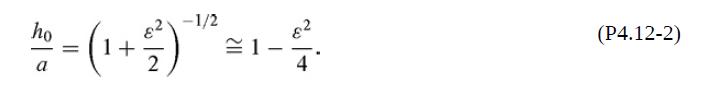

Use is made here of (1 + x)^1/2 = 1 + x/2 + ⋅⋅⋅ and (1 + x)⁻¹ = 1 − x + ⋅⋅⋅, where the terms involving higher powers of x are neglected. Thus, the average radius of the wavy cylinder is slightly less than the unperturbed radius.

(b) The change in interfacial area per wavelength is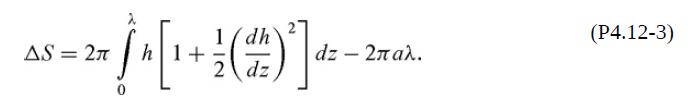

Show that ΔS < 0 for λ > 2πa and any small value of ε. Accordingly, the cylindrical surface is unstable with respect to any long-wavelength disturbance, no matter how small its initial amplitude. The amplitude grows until the film forms the string of “pearls” in Fig. P4.12(b). How to calculate the final droplet shape is discussed in De Gennes et al. (2003, p. 11).

Notice that the critical wavelength is independent of the fiber radius b. Indeed, the key parts of the derivation are unchanged if there is no inner cylinder at all. A critical wavelength λ = πd(where d is the diameter of a liquid cylinder) was discovered experimentally by the Belgian physicist Joseph Plateau about 1870 and later confirmed theoretically by Lord Rayleigh. As described in De Gennes et al. (2003, pp. 119–120), Plateau found that oil droplets immersed in water could be made to coalesce into cylinders by pushing them together. However, the cylinders broke up when λ/d was greater than 3.13 to 3.18. Of importance for technologies such as inkjet printing is that a cylindrical jet of liquid also starts to break up as soon as its length exceeds its circumference.

Transcribed Image Text:

a 2b Z=0 h(z) (a) Z=λ | ho (b) Figure P4.12 Plateau-Rayleigh instability. A liquid film that coats small wettable fiber, as in (a), rearranges spontaneously into a string of droplets, as in (b).