The arrangement in Fig. P8.10 is well suited for determining the viscosity of small liquid samples. An inverted cone of radius R and small angle β is brought into contact with a pool of the liquid on a flat plate, and μ is determined by measuring the torque required to rotate the cone at a constant angular velocity ω. Stokes’ equation is applicable and spherical coordinates are useful, as shown.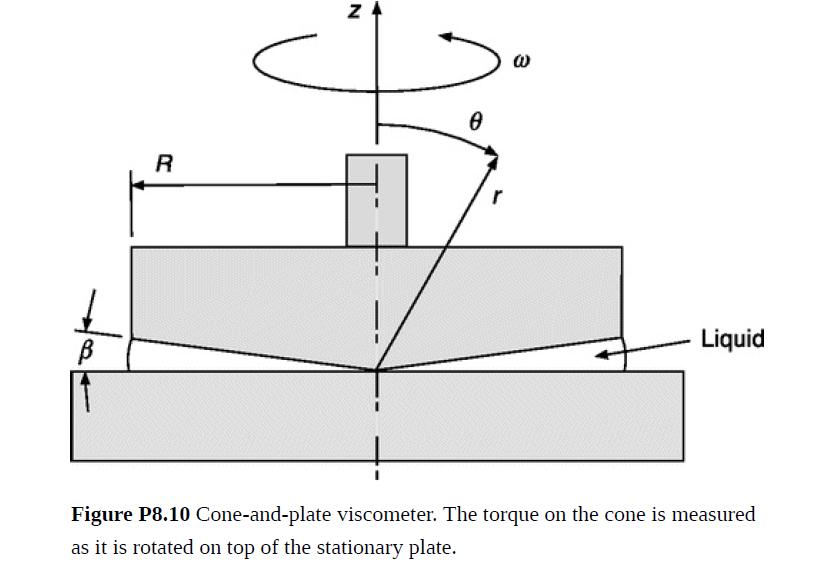

(a) Show that a velocity field with v_ϕ(r, θ) = rf(θ) and v_r = v_θ = 0 is consistent with conservation of mass, conservation of momentum, and the boundary conditions at the solid surfaces. Derive the differential equation and boundary conditions for f(θ).

(b) Simplify the governing equations for f(θ) for β ≪ 1 and evaluate v_ϕ(r, θ).

(c) The torque applied to the cone must equal that on the plate. Show that the torque G on the plate is

Transcribed Image Text:

↓ В R N 0 Liquid Figure P8.10 Cone-and-plate viscometer. The torque on the cone is measured as it is rotated on top of the stationary plate.