Suppose that an extremely viscous liquid fills a space of thickness H between two disks of radius R, as shown in Fig. P8.9. The upper disk rotates at a constant angular velocity ω and the lower one is fixed. Inertia is negligible because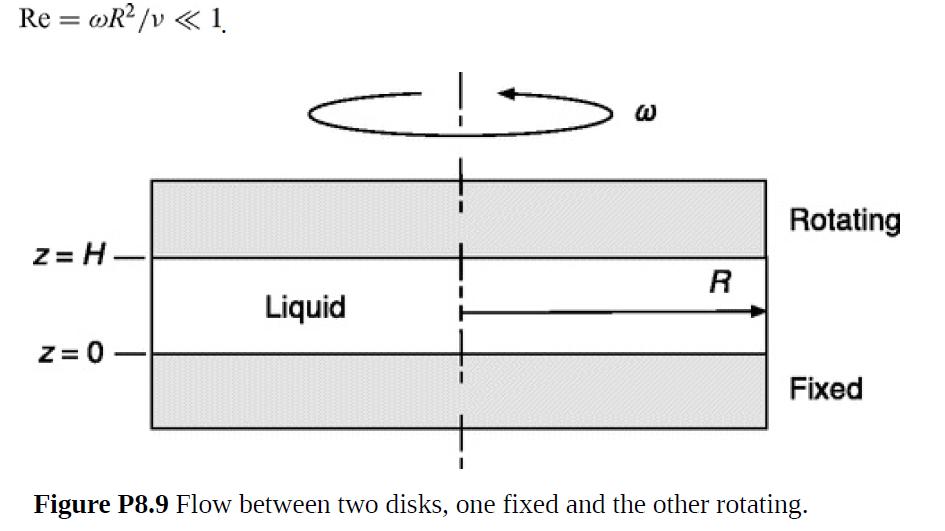

(a) Show that there is a solution to the θ component of Stokes’ equation of the form v_θ(r, z) = rf(z) and determine f(z).

(b) Show that all the other equations are satisfied if v_r = v_z = 0 and ℘ is constant. This confirms that this creeping flow is unidirectional (i.e., purely rotational).

(c) Calculate the torque that must be applied to the upper disk to maintain its rotation.

Transcribed Image Text:

Re = R² /v << 1 z=H_ Z=0- Liquid ļ W R Rotating Fixed Figure P8.9 Flow between two disks, one fixed and the other rotating.