The objective is to estimate the drag on a cylinder from the velocity reduction measured in its wake. The cylinder of diameter d and length L (≫ d) is perpendicular to the approaching flow. Figure P11.5 shows a control volume that includes half the system of interest. It extends from a position upstream from the cylinder (S₁, where v_x = U) to one many diameters downstream (S₂, where v_x is measured). To ensure that v_x = U everywhere on S₃, let H → ∞. Except for the part that coincides with the top of the cylinder, S₄ is a symmetry plane.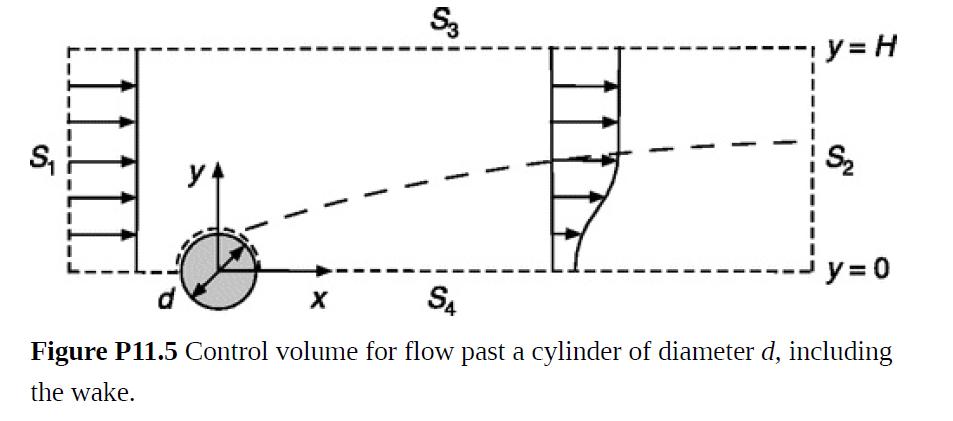

(a) Show that the outward flow rate through S₃ is given by an expression like Eq. (P11.4-1).

(b) Show that the drag can be calculated much as in Eq. (P11.4-2).

(c) Of particular interest is the velocity reduction at S₂, Λ(x, y) = U − v_x(x, y). If Λ/U ≪ 1, show that the drag coefficient for the full cylinder is given by

(d) Townsend (1949) mounted a wire with d = 0.159 cm in a wind tunnel. For U = 12.80 m/s, corresponding to Re = 1360, he measured wake velocities at positions within the range 500 ≤ x⁄d ≤ 950. The data were represented fairly well (although not exactly) by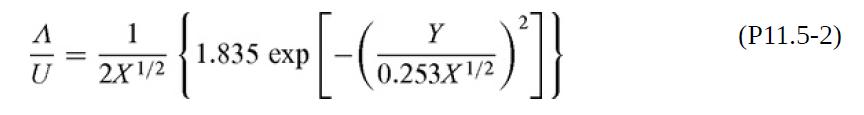

where Y = y⁄d, X = (x − x₀)/d, and x₀/d = 90. Evaluate C_D from this information. [Equation (P11.4-5) will be helpful.] 

Transcribed Image Text:

1.11 - $3 q y=H S₂ y = 0 X S₁ Figure P11.5 Control volume for flow past a cylinder of diameter d, including the wake.