The drag on an object can be inferred from the velocity reduction in its wake. Figure P11.4 depicts the boundary layer and wake on one side of a flat plate. The surfaces S₁ through S₄ enclose a control volume that extends from y = 0 to y = H and from a position upstream from the leading edge (where v_x = U) to one downstream from the trailing edge. To ensure that v_x = U everywhere on S₃, let H → ∞. The plate length is L and its width is W.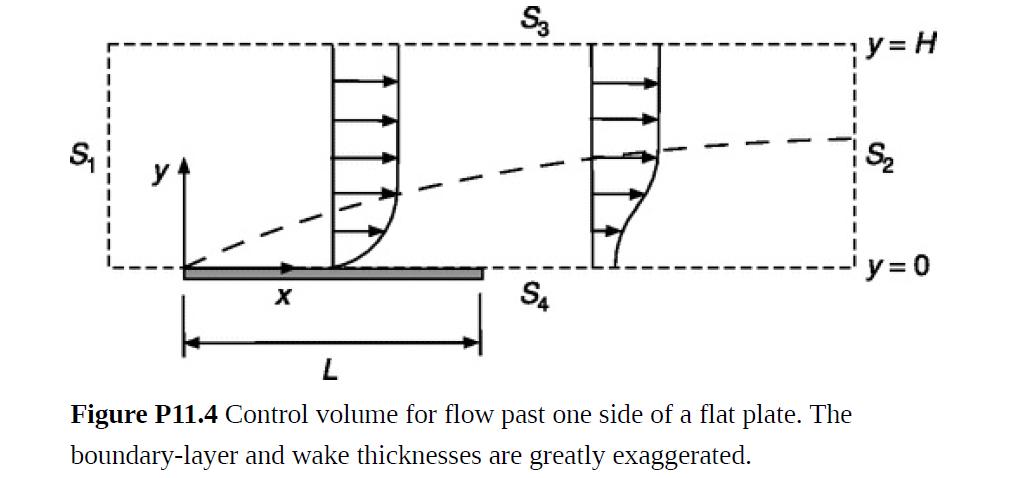

(a) Show that the outward volume flow rate through S₃ is related to U and the velocity v_x evaluated on S₂ as

(b) Show that the drag on one side of the plate is

where v_x again is evaluated on S₂.

(c) For x⁄L > 3, it has been found that the velocity reduction, Λ(x, y) = U − v_x(x, y), is represented accurately by (Schlichting, 1968, p. 169)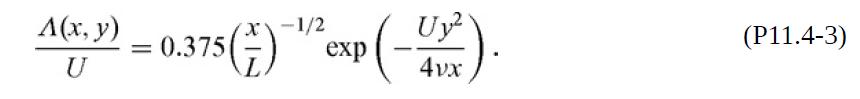

For x large enough that Λ/U ≪ 1, v_x≅U and the result in part (b) can be simplified to

Use this to calculate C_f and compare your result with that in Example 9.3-1. A definite integral that is helpful here is

Transcribed Image Text:

X S3 S4 L Figure P11.4 Control volume for flow past one side of a flat plate. The boundary-layer and wake thicknesses are greatly exaggerated. y = H S₂ y = 0