The setup in Fig. P12.8 was used to help characterize porous membranes employed in diffusion studies (Epstein, 1979). The membrane hydraulic permeability k_m obtained using this apparatus was used to find the pore diameter d. If a transmembrane pressure difference |ΔP|_m gives a volume flow rate Q through a membrane of area S_m, then k_m = Q/(S_m|ΔP|_m). After a reservoir was placed at a measured height H, Q was found by timing the movement of the meniscus in a pipette placed at the outlet. The cross-sectional area of the outlet was S_o.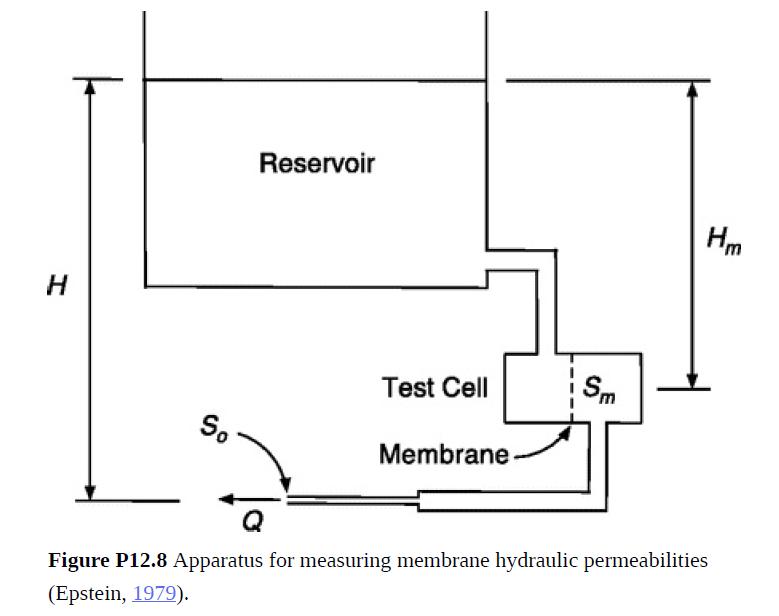

(a) The membranes had straight cylindrical pores and the pore number density n (number of pores per unit area) and pore length L for each membrane were measured separately. If Poiseuille's law applies to each pore, show how to calculate d from k_m, n, and L. With H = 20 cm, d = 80 nm, and L = 6.0 μm being typical, why was it reasonable to assume fully developed laminar flow in the pores?

(b) If the membrane were the only resistance to flow, how could k_m be calculated from the dependence of Q on H?

(c) It was suspected that resistances in other parts of the apparatus were not always negligible, especially for relatively large pore sizes and high flow rates. Accordingly, Q was measured as a function of H with no membrane present. The extramembrane loss E_{v, o} was expressed as

where F is dimensionless and v_o = Q/S_o is the mean velocity at the outlet. Show how to evaluate F from such data. In contrast to turbulent flow, where loss coefficients are nearly constant, in this laminar-flow apparatus F was sensitive to Q. (It was found to vary as Re^–1.24, where Re is the outlet Reynolds number.)

(d) With F a known function of Re, show how to find k_m from the original experiments.

Transcribed Image Text:

H So- Reservoir Test Cell Membrane Sm Hm Figure P12.8 Apparatus for measuring membrane hydraulic permeabilities (Epstein, 1979).