The fundamental internal energy relation for a rubber band is dU = TdS - FdL where F is the system force, which is negative when the rubber band is in tension. The applied force is given by F_applied = k(T)(L – L_o) where k(T ) is positive and increases with increasing temperature. The heat capacity at constant length is given by C_L = α(L) + β(L)·T. Stability arguments show that α(L) and β(L) must provide for C_L ≥ 0.

(a) Show that temperature should increase when the rubber band is stretched adiabatically and reversibly.

(b) Prof. Lira in his quest for scientific facts hung a weight on a rubber band and measured the length in the laboratory at room temperature. When he hung the rubber band with the same weight in the refrigerator, he noticed that the length of the rubber band had changed. Did the length increase or decrease?

(c) The heat capacity at constant force is given by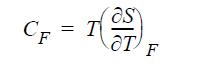

Derive a relation for C_F - C_L and show whether this difference is positive, negative, or zero.

(d) The same amount of heat flows into two rubber bands, but one is held at constant tension and the other at constant length. Which has the largest increase in temperature?

(e) Show that the dependence of k (T) on temperature at constant length is related to the dependence of entropy on length at constant temperature. Offer a physical description for the signs of the derivatives.

Transcribed Image Text:

CF = || T as ST F