The truncated virial equation (density form) is Z = B + 1 According to Eqn. 7.52, the
Question:
The truncated virial equation (density form) is Z = Bρ + 1 According to Eqn. 7.52, the virial coefficient is given by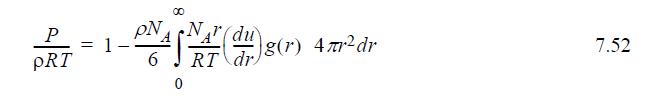

where the low pressure limit of g(r) given by Eqn. 7.57 is to be used. Another commonly cited equation for the virial coefficient is Eqn. 7.59. Show that the two equations are equivalent by the following steps:![u(r) exp[-] lim g(r) exp P0 7.57](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1696/0/6/2/5176517dc35409411696062515236.jpg)
(a) Beginning with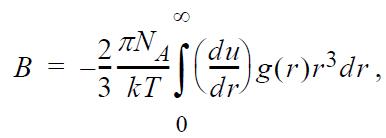
insert the low-pressure limit for g(r), and simplify as much as possible.
(b) Integrate by parts to obtain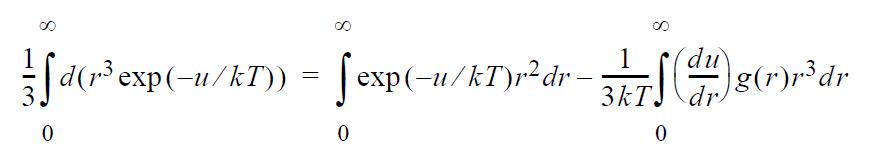
(c) Show that the left-hand side of the answer to part (b) may be written as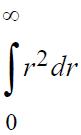
for a physically realistic pair potential. Then combine integrals to complete the derivation of Eqn. 7.59.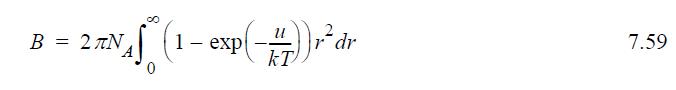
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Introductory Chemical Engineering Thermodynamics
ISBN: 9780136068549
2nd Edition
Authors: J. Elliott, Carl Lira
Question Posted:





