Two special models of liquid-solution behavior are the regular solution, for which S^E = 0 everywhere, and the a thermal solution, for which H^E = 0 everywhere.

(a) Ignoring the P-dependence of G^E, show that for a regular solution,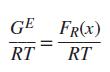
(b) Ignoring the P-dependence of G^E, show that for an athermal solution,
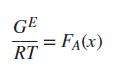(c) Suppose that G^E∕RT is described by the symmetrical equation
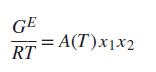From parts (a) and (b), we conclude that where α and β are constants.

What are the implications of Eqs. (A) and (B) with respect to the shapes of predicted solubility diagrams for LLE? Find from Eq. (A) an expression for the consolute temperature, and show that it must be an upper consolute temperature.

Suggestion: See Ex. 15.3 for numerical guidance.

Example 15.3

The simplest expression for G^E ∕RT capable of predicting LLE is:

Derive the equations resulting from application of this equation to LLE.

GE FR(X) RT RT