Consider a plane loop of wire that carries a steady current I; we want to calculate the magnetic field at a point in the plane. We might as well take that point to be the origin (it could be inside or outside the loop). The shape of the wire is given, in polar coordinates, by a specified function r (θ) (Fig. 5.62).

(a) Show that the magnitude of the field is26

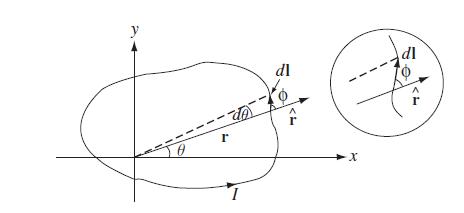
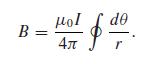
(b) Test this formula by calculating the field at the center of a circular loop.
(c) The “lituus spiral” is defined by (for some constant a). Sketch this figure, and complete the loop with a straight segment along the x axis. What is the magnetic field at the origin?

(d) For a conic section with focus at the origin where p is the semilatus rectum (the y intercept) and e is the eccentricity (e = 0 for a circle, 0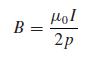

IP X+ r IP UP J TO y