First write B(r) as a Taylor expansion about the center of the loop: where r₀ is the position of the dipole and ∇0 denotes differentiation with respect to r₀. Put this into the Lorentz force law (Eq. 5.16) to obtain

Or, numbering the Cartesian coordinates from 1 to 3:

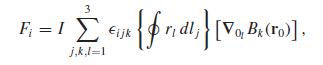
where i j k is the Levi-Civita symbol (+1 if i j k = 123, 231, or 312; −1 if i j k = 132, 213, or 321; 0 otherwise), in terms of which the cross-product can be written (A × B)_{i =}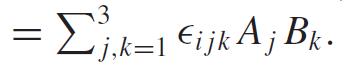

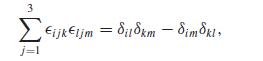
B(r) = B(ro) + [(r-ro) Vo]B(ro),