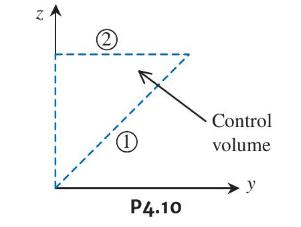
The velocity field in the region shown is given by \(\vec{V}=(a \hat{j}+b y \hat{k})\) where \(a=10 \mathrm{~m} / \mathrm{s}\) and \(b=5 \mathrm{~s}^{-1}\). For the \(1 \mathrm{~m} \times 1 \mathrm{~m}\) triangular control volume (depth \(w=1 \mathrm{~m}\) perpendicular to the diagram), an element of area (1) may be represented by \(d \overrightarrow{A_{1}}=w d z \hat{j}-w d y \hat{k}\) and an element of area (2) by \(d \overrightarrow{A_{2}}=-w d y \hat{k}\).

(a) Find an expression for \(\vec{V} \cdot d A_{1}\).

(b) Evaluate \(\int_{A_{1}} \vec{V} \cdot d A_{1}\).

(c) Find an expression for \(\vec{V} \cdot d A_{2}\).

(d) Find an expression for \(\vec{V}\left(\vec{V} \cdot d A_{2}\right)\).

(e) Evaluate \(\int_{A_{2}} \vec{V}\left(\vec{V} \cdot d A_{2}\right)\).

Transcribed Image Text:

2 1 1 1 P4.10 Control volume y