A continuous random variable is said to have a Rayleigh distribution with parameter if its PDF is given by where 0 a If X Rayleigh(), find EX b If X Rayleigh(), find the CDF of X,F X (x) c If X Exponential(1) and Y 2 2 X, show that Y Rayleigh() X x 20 fx(x) e 02 x 20 0 u(x) if x 0 if x 0

Question: A continuous random variable is said to have a Rayleigh distribution with parameter if its PDF is given by where > 0. a.

A continuous random variable is said to have a Rayleigh distribution with parameter σ if its PDF is given by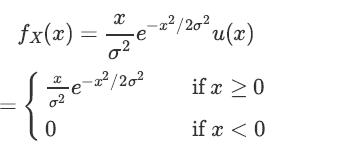 X -x/20 fx(x) e 02 -x/20 {** 0 u(x) if x 0 if x < 0

where σ > 0.

a. If X ∼ Rayleigh(σ), find EX.

b. If X ∼ Rayleigh(σ), find the CDF of X,F_X(x).

c. If X ∼ Exponential(1) and Y = √2σ²X, show that Y ∼ Rayleigh(σ).

X -x/20 fx(x) e 02 -x/20 {** 0 u(x) if x 0 if x < 0

Step by Step Solution

★★★★★

3.50 Rating (153 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a Finding the expected value of X The expected value of X denoted by EX is given by the following integral EX x fx dx where fx is the PDF of X In this ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Introduction To Probability Statistics Questions!

15. The Investment Club at Bell Labs has solicited and obtained $50,000 from its members. Collectively, the members have selected the three stocks, two bond funds, and a tax-deferred annuity shown in...

A continuous random variable is said to have a Laplace(, b) distribution [ 14 ] if its PDF is given by

A continuous random variable is said to have a Pareto(x m ,) distribution [ 15 ] if its PDF is given by where x m , > 0. Let X Pareto(x m ,). a. Find the CDF of X, FX(x). b. Find P(X > 3x m |X > 2x...

A continuous random variable is said to have a Rayleigh distribution with parameter o if its PDF is given by for a >= 0 fx (x) = o2 for a

Probability and Random Processes. A continuous random variable is said to have a Rayleigh distribution with parameter o if its PDF is given by for a >= 0 fx(x): o2 for a

Arandom variable X is said to have a Rayleigh distribution with parameter > 0 (frequently encountered when modelling wireless communication systems) if its pdf is of the form fX(x) = x 2 exp{ x2 22...

I need someone to check the solutions to Q9,10,11 and 12. View the questions and solutions down below. Questions: XY XY 1,1 2,1 3, 1 4127 5717 6127 2 . 2 3,2 4, 2 512- 6,2 1,2 1,3 2 ,3 3,3 4, 3 5,3...

kindly solve the question step by step and solve all the parts. I have give all the information.kindly solve question as soon as possible. 2. Let fX,Y(x,y)={Cexp(21(x2+y2))0if0xyotherwise (a) Compute...

Decision Sciences LeBow College of Business Drexel University 3220 Market Street Philadelphia, PA 19104 STAT 201 - Business Statistics I Final Name (Last, First) : Student ID Card# : Part I. T/F...

Determine if the given statements in (1)-(10) are true or false (circle your answer). 1. For independent random variables X and Y , we have that Var(X+ Y ) = Var(X) + Var(Y ). 2. Let Y = 3X1 + 2X2...

Explain the basic difference between psychological egoism and ethical egoism.

"TCL is not the market leader. Explain with Porter Competitive Edge Theory"

What is the weighted average cost of capital ( WACC ) , and how is it calculated? What is the relationship between the firm s target capital structure and the weighted average cost of capital ( WACC...

466 Using no more than two OP AMPs, design an OP AMP circuit with inputs v1, v2, and 100 mV and an output vO = 3v1 + 2v2 300 mV.

Thermal resistance tests on 13 samples of Enterococcus hirae, present in milk, yield the following results in degrees Celsius: Another set of seven samples of milk was tested after pasteurization to...

Past data indicate that the variance of measurements made on sheet metal stampings by experienced quality-control inspectors is 0.18 (inch) ${ }^{2}$. Such measurements made by an inexperienced...

If 44 measurements of the refractive index of a diamond have a standard deviation of 2.419 , construct a 95% confidence interval for the true standard deviation of such measurements. What assumptions...

On April 1, 2019, Alaska Trading Company issued $900,000 of 6%, 10-year bonds. The bonds, which were issued at 98, pay interest on October 1 and April 1. Use this information to prepare the General...

What is the treatment of the following items in connection with the retail inventory method? g. Sales return h. Employee discount 1. Normal and abnormal shortage, shrinkage, spoilage and breakage

20.Which one of the following has the lowest effective annual rate? a. 6 percent compounded annually b. 6 percent compounded semiannually c. 6 percent compounded quarterly d. 6 percent compounded...