Alice wants to buy a new iPad, and she would like to try her chances with the lottery for the first time. After a little research, she finds out that a single ticket of the lottery (i.e. if you select just 6 numbers out of the 49) costs $1, while in order to win enough money to buy the iPad, she must predict at least 4 numbers, out of the 6 drawn, correctly. She feels that, if she buys a single ticket, her chances are very slim. She therefore decides to select eight numbers and, because she is quite good at maths (and also, she has just finished a course in Probability), she works out that she has to pay $28 (she is right, but explain why!). Then, she wants to find out what are her chances of predicting exactly four out of the six numbers in the next draw, and she comes up with an answer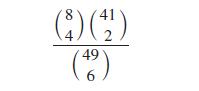

(she is right again, as you can verify). After that, she meets her friend Bill and tells him that she bought a ticket with eight numbers for the next lottery draw, but doesn’t tell him what these numbers are.
On the night of the draw, Bill watches his favorite program on television and suddenly the six numbers drawn in the lottery appear on the screen. She remembers what Alice told him and wants to find out what are the chances that she won, so he argues as follows.
Alice may have chosen any 8 out of the 49 numbers, and there are (49 8) ways to do this. The favorable outcomes (remember that he knows only the numbers drawn, not the ones that Alice chose) are (6 4 )
(since Alice must have picked 4 numbers of the 6 drawn) multiplied by (43 4 )
, since the other 4 numbers on Alice’s ticket are not winning numbers. Therefore, Bill thinks that the probability that Alice has picked four correct numbers is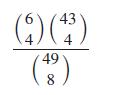

Show that this result agrees with Alice’s result above.
The fact that the two results agree is an immediate consequence of the combinatorial identity

for any positive integers N, n,

b, x such that x ≤ min{n, b} and N ≥ max{n, b}.
Verify this identity!

Transcribed Image Text:

(4)(4) 49 6