Canada has a Road Safety Vision of having the safest roads in the world. Yet the lead- ing cause of death of Canadian children remains vehicle crashes. In 2006, a national child safety seat survey was conducted by an AUTO21 research team in collaboration with Transport Canada to empirically measure Canada's progress towards achieving Road Safety Vision 2010. Child seat use was observed in parking lots and nearby in- tersections in 200 randomly selected sites across Canada. The following table provides a classification of a subset of children in the survey by age groups and type of restraint device they were using at the time of the survey.

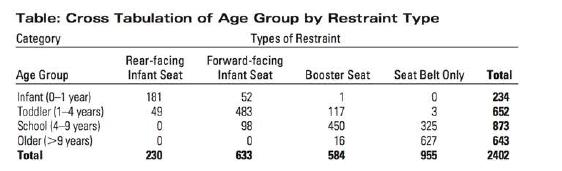
a. Which statistical technique is appropriate to describe the above data?

b. What is the sampling distribution of the test statistic for a goodness-of-fit test with these categories?

c. Suppose you wish to test whether the types of restraint are related to age group. (i) State the appropriate hypotheses. (ii) Which test statistic will you use to test the hypotheses in part (i)? What will be the sampling distribution of your test statistic? (iii) At a glance on the table, what difficulty, if any, do you expect to encounter in calculating the test statistics for the hypotheses in part (i)? (iv) Write a short report explaining the issues in performing a formal test on the hypothesis in part (i). In other words, what are the statistical issues? (v) What remedies will you suggest to alleviate the problems you came across in calculating the test statistic? Make some necessary recommendations to the researcher for a future survey.

d. Let us consider the following adjusted data with fixed column total in the following table:

Suppose you wish to test the null hypothesis that the three binomial parameters PA PB, and Pc are equal versus the alternative hypothesis that at least two of the parameters differ. (i) Write the null and alternative hypotheses for testing the equality of the three binomial proportions. (ii) Calculate the test statistic and find the approximate p-value for the test in the previous question. (iii) Use the approximate p-value to determine the statistical significance of your results. If the results are statistically significant, explore the nature of the differences in the three binomial proportions. (iv) If there are more than two row categories in a contingency table with fixed- total c columns, then the test of independence is equivalent to a test of the equality of c sets of multinomial proportions. Justify your answer.

Transcribed Image Text:

Table: Cross Tabulation of Age Group by Restraint Type Category Types of Restraint Age Group Rear-facing Infant Seat Forward-facing Infant Seat Booster Seat Seat Belt Only Total Infant (0-1 year) 181 Toddler (1-4 years) 49 School (4-9 years) Older (>9 years) 0 0 52 1 0 234 483 98 117 3 652 450 325 873 0 16 627 643 Total 230 633 584 955 2402