Consider the co ntinuous Markov chain of Example 11.17: A chain with two states S = {0, 1} and λ₀ = λ₁ = λ > 0. In that example, we found that the transition matrix for any t ≥ 0 is given by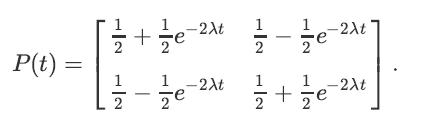

a. Find the generator matrix G.

b. Show that for any t ≥ 0, we have

where P ′(t) is the derivative of P(t).

Example 11.17

Consider a continuous Markov chain with two states S = {0, 1}. Assume the holding time parameters are given by λ₀ = λ₁ = λ > 0. That is, the time that the chain spends in each state before going to the other state has an Exponential(λ) distribution.

Transcribed Image Text:

P(t) = + -2Xt 1-2Xt ze 1 2 글 + e -2Xt -2Xt