Consider the unit disc D = {(x, y)|x 2 +y 2 1}. Suppose that we choose
Question:
Consider the unit disc D = {(x, y)|x2 +y2 ≤ 1}. Suppose that we choose a point (X, Y) uniformly at random in D. That is, the joint PDF of X and Y is given by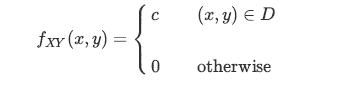
a. Find the constant c.
b. Find the marginal PDFs fX(x) and fY (y).
c. Find the conditional PDF of X given Y = y, where −1 ≤ y ≤ 1.
d. Are X and Y independent?
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
a We have 1 b For 1 x 1 we have Thus c 1 c D fxr2ydxdy c dxdy carea of D C fxx fxx ...View the full answer
Answered By
Nicholas Maina
Throughout my tutoring journey, I've amassed a wealth of hands-on experience and honed a diverse set of skills that enable me to guide students towards mastering complex subjects. My proficiency as a tutor rests on several key pillars:
1. Subject Mastery:
With a comprehensive understanding of a wide range of subjects spanning mathematics, science, humanities, and more, I can adeptly explain intricate concepts and break them down into digestible chunks. My proficiency extends to offering real-world applications, ensuring students grasp the practical relevance of their studies.
2. Individualized Guidance:
Recognizing that every student learns differently, I tailor my approach to accommodate various learning styles and paces. Through personalized interactions, I identify a student's strengths and areas for improvement, allowing me to craft targeted lessons that foster a deeper understanding of the material.
3. Problem-Solving Facilitation:
I excel in guiding students through problem-solving processes and encouraging critical thinking and analytical skills. By walking learners through step-by-step solutions and addressing their questions in a coherent manner, I empower them to approach challenges with confidence.
4. Effective Communication:
My tutoring proficiency is founded on clear and concise communication. I have the ability to convey complex ideas in an accessible manner, fostering a strong student-tutor rapport that encourages open dialogue and fruitful discussions.
5. Adaptability and Patience:
Tutoring is a dynamic process, and I have cultivated adaptability and patience to cater to evolving learning needs. I remain patient through difficulties, adjusting my teaching methods as necessary to ensure that students overcome obstacles and achieve their goals.
6. Interactive Learning:
Interactive learning lies at the heart of my approach. By engaging students in discussions, brainstorming sessions, and interactive exercises, I foster a stimulating learning environment that encourages active participation and long-term retention.
7. Continuous Improvement:
My dedication to being an effective tutor is a journey of continuous improvement. I regularly seek feedback and stay updated on educational methodologies, integrating new insights to refine my tutoring techniques and provide an even more enriching learning experience.
In essence, my hands-on experience as a tutor equips me with the tools to facilitate comprehensive understanding, critical thinking, and academic success. I am committed to helping students realize their full potential and fostering a passion for lifelong learning.
5+ Reviews
16+ Question Solved
Related Book For 
Introduction To Probability Statistics And Random Processes
ISBN: 9780990637202
1st Edition
Authors: Hossein Pishro-Nik
Question Posted:
