Let X and Y be as in Example 5.24 in Section 5.2.3, i.e., suppose that we choose a point (X,Y ) uniformly at random in the unit disc 

Are X and Y uncorrelated?

Example 5.24 in Section 5.2.3

Consider the unit disc D = {(x, y)|x² +y² ≤ 1}.

Suppose that we choose a point (X,Y ) uniformly at random in D. That is, the joint PDF of X and Y is given by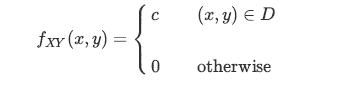

a. Find the constant c.

b. Find the marginal PDFs f_X(x) and f_Y (y).

c. Find the conditional PDF of X given Y = y, where −1 ≤ y ≤ 1.

d. Are X and Y independent?

Transcribed Image Text:

D = {(x, y)|x² + y² ≤ 1}.