Let X be a continuous random variable with density function f . We say that X has
Question:
Let X be a continuous random variable with density function f . We say that X has a symmetric distribution around the point a if we have P(X ≥ a + x) = P(X ≤ a − x)
for any x ∈ ℝ.
(i) Show that the distribution of X is symmetric around a if and only if f (a − x) = f (a + x).
(ii) Establish that each of the following distributions, with densities given below, is symmetric around a point a which should be identified: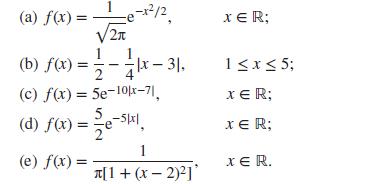
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Introduction To Probability Volume 2
ISBN: 9781118123331
1st Edition
Authors: Narayanaswamy Balakrishnan, Markos V. Koutras, Konstadinos G. Politis
Question Posted:






