Let {X(t), t R} be a continuous-time random process. The time average mean of X(t) is

Question:

Let {X(t), t ∈ R} be a continuous-time random process. The time average mean of X(t) is defined as (assuming that the limit exists in mean-square sense)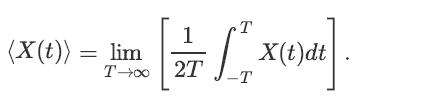 (X(t)) = lim T [ 1 2T T -T X(t)dt

Consider the random process {X(t), t ∈ R} defined as

where U ∼ Uniform(0, 2π). Find ⟨X(t)⟩.

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Introduction To Probability Statistics And Random Processes

ISBN: 9780990637202

1st Edition

Authors: Hossein Pishro-Nik

See More Books

Question Posted: Nov 01, 2023 01:41 PM

See More Questions

Let I := [a, b and let f : I R be a continuous function such that f(x) > 0 for each x in I. Prove that there exists a number a > 0 such that f(x) > a for all x I.
Write a MARIE program to encode your name and ID as a string The following example of a MARIE string "nameID" encodes a name and an ID using ASCII characters. The "name" is separated from the ID by...
Let I := [a, b] and let f : I R be a continuous function on I such that for each x in I there exists y in I such that | f (y)| < | f(x)|. Prove there exists a point c in I such that f(c) = 0.
Prepare a statement of cash flows in proper form using the inflows and outflows from questions 4-15. Assume net income (earnings after taxes) from the 2018 income statement was $10,628, and $5,000 in...
Croftmark Co. began operations on May 1, 2010. Its Work in Process Inventory account on May 31 appeared as follows: The company applies overhead on the basis of direct labor cost. Only one job was...
Helen Knight is attempting to sell her business to Chris Bosh. The company has assets of $1,800,000, liabilities of $1,600,000, and owners equity of $200,000. Both parties agree that the proper rate...
Emotions are often associated with events that are easily remembered. The link between emotions and memory has been demonstrated behaviorally and physiologically. The amygdala is a key structure for...
1. Based on the information given, summarize the method(s) BMW intends to use for determining incentive pay. Are these rewards for individual, group, and/or company performance? 2. Explain BMWs claim...
What price should be paid for a $10,000 Government of Ontario strip bond with 17 years remaining to maturity if it is to yield the buyer 2.770% compounded semiannually? A trust company pays 5.375%...
Let X(t) be a zero-mean Gaussian random process with R X () = 8 sinc(4). Suppose that X(t) is input to an LTI system with transfer function If Y (t) is the output, find P(Y (2) H(f) = 2 0 |f| <1...
In some applications, we need to work with complexvalued random processes. More specifically, a complex random process X(t) can be written as X(t) = X r (t) +jX i (t), where X r (t) and X i (t) are...
In the simplified model with proportional taxation there can be two equilibria, one with a high tax rate and one with a low tax rate. Now, suppose that government spending increases. Determine the...
1. While improper framing could affect the information we have on sark attacks, I think our decisions come down to "anchoring and adjustment". Because the information we received from the media was...
For each of the scenarios in the following table, indicate the most likely reason for the difference in earnings. Scenario Differences in Human Capital Compensating Differential Differences in...
All organizations whether it is the government, a private business or small businessman require planning. To turn their dreams of increase in sale, earning high profit and getting success in business...
A parent acquires all of the stock of a subsidiary for $40 million in cash. The subsidiarys books report the following account balances at the date of acquisition (in trial balance format)....
1. Given: The sign for the Inn of the Prancing Pony in Bree-yes, it comes in pints-is fixed on the end of a beam of length 5L. If the sigh deflects too much then Gandalf will hit his head when he...
Discuss the income elasticities of the following consumer products: a. Margarine b. Fine jewelry c. Living room furniture d. Whole lobsters
You are planning to purchase your first home five years from today. The required down payment will be $50,000. You currently have $20,000. but you plan to contribute $500 each quarter to a special...
As a library or internet assignment, find the U.S. productivity rate (increase) last year for the (a) national economy, (b) manufacturing sector, (c) service sector.
Solutions Corporation, a computer vendor and consulting company, uses the accrual method of accounting. Its tax year is the calendar year. The following are three of the corporations transactions...
Pamello, Inc., an engineering consulting firm, uses the cash method of accounting and is a calendar year taxpayer. Compute the amount of Pamellos current year deductions for the following...
Virgil Watson gave his daughter, Holly, a gift of passive activity property. Suspended losses amounted to $30,000 and the property had an adjusted basis of $40,000. Also, the property had a fair...
2. Turkey Corp. has a computer that they purchased on March 30, 2016, for $ 106,000. This computer had an estimated life of ten years and a residual value of $ 6,000. On December 31, 2020, the old...
Explain the steps in the posting process. Also, discuss what a Trial balance is and why it is an important step in the accounting cycle. Does a trial balance that is in balance guarantee that all...

Let {X(t), t R} be a continuous-time random process. The time average mean of X(t) is

Question:

(X(t)) = lim T→∞ [ 1 2T T -T X(t)dt

Step by Step Answer:

The time average mean of a continuoustime random process Xt t R is defined as follows Equation 1 Xt ...View the full answer

Introduction To Probability Statistics And Random Processes

Students also viewed these Business questions