When the choice of a prior distribution is subjective, it is often advantageous to choose a prior distribution that will result in a posterior distribution of the same distributional family. When the prior and posterior distributions share the same distributional family, they are called conjugate distributions, and the prior is called a conjugate prior. Conjugate priors are used out of ease because they always result in a closed form posterior distribution. One example of this is to use a gamma prior for Poisson distributed data. Assume our data Y given X is distributed Y | X = x ∼ Poisson(λ = x) and we chose the prior to be X ∼ Gamma(α,β). Then the PMF for our data is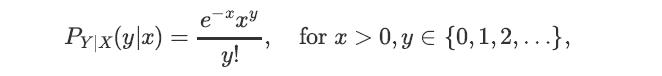

and the PDF of the prior is given by

a. Show that the posterior distribution is Gamma(α +y,β +1). Remove all the terms not containing x by putting them into some normalizing constant, c, and noting that f_X|Y (x|y) ∝ P_Y|X(y|x)f_X(x).)

b. Write out the PDF for the posterior distribution, f_X|Y (x|y).

c. Find mean and variance of the posterior distribution, E[X|Y] and Var(X|Y).

Transcribed Image Text:

Py|x(y|x) = = e-х ху y! for x > 0,y ∈ {0,1,2,...},