Consider operators A and B that do not commute with each other but do commute with their
Question:
Consider operators  and B̂ that do not commute with each other ![]() but do commute with their commutator:
but do commute with their commutator:
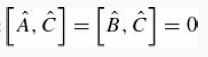
(for instance, x̂ and p̂).
(a) Show that

You can prove this by induction on n, using Equation 3.65.
(b) Show that
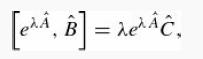
where λ is any complex number. Express eλ as a power series.
(c) Derive the Baker–Campbell–Hausdorff formula:
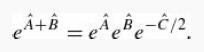
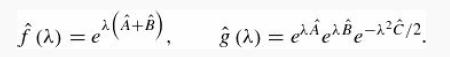
these functions are equal at λ = 0, and show that they satisfy the same differential equation:
![]()
and
![]()
Therefore, the functions are themselves equal for all λ.
Equation 3.65
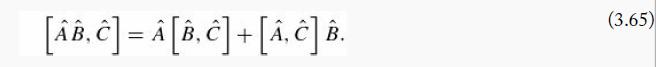
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Introduction To Quantum Mechanics
ISBN: 9781107189638
3rd Edition
Authors: David J. Griffiths, Darrell F. Schroeter
Question Posted:





