In Section 5.1 we found that for noninteracting particles the wave function can be expressed as a product of single-particle states (Equation 5.9)—or, for identical particles, as a symmetrized/antisymmetrized linear combination of such states (Equations 5.20 and 5.21). For interacting particles this is no longer the case. A famous example is the Laughlin wave function, which is an approximation to the ground state of N electrons confined to two dimensions in a perpendicular magnetic field of strength B (the setting for the fractional quantum Hall effect). The Laughlin wave function is

where q is a positive odd integer and

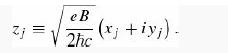
(Spin is not at issue here; in the ground state all the electrons have spin down with respect to the direction of B, and that is a trivially symmetric configuration.)
(a) Show that has the proper antisymmetry for fermions.
(b) For q = 1, Ψ describes noninteracting particles (by which I mean that it can be written as a single Slater determinant—see Problem 5.8). This is true for any N, but check it explicitly for N = 3. What single particle states are occupied in this case?
(c) For values of q greater than 1, Ψ cannot be written as a single Slater determinant, and describes interacting particles (in practice, Coulomb repulsion of the electrons). It can, however, be written as a sum of Slater determinants. Show that, for q = 3 and N = 2, Ψ can be written as a sum of two Slater determinants.
In the noninteracting case (b) we can describe the wave function as “three particles occupying the three single-particle states Ψ_a, Ψ_b and Ψ_c,” but in the interacting case (c), no corresponding statement can be made; in that case, the different Slater determinants that make up Ψ correspond to occupation of different sets of single-particle states.

Equation 5.9

Equations 5.20

Equations 5.21

N N II 2.) ] exp[- + $1] _j