In this problem you will show that the number of nodes of the stationary states of a one-dimensional potential always increases with energy. Consider two (real, normalized) solutions (Ψ_n and Ψ_m) to the time-independent Schrödinger equation (for a given potential V (x) ), with energies E_n < E_m.

(a) Show that

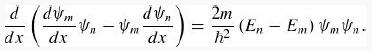
(b) Let x₁ and x₂ be two adjacent nodes of the function Ψ_m (x). Show that

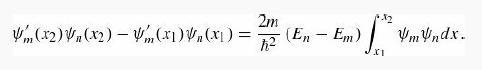
(c) If Ψ_n (x) has no nodes between and , then it must have the same sign everywhere in the interval. Show that (b) then leads to a contradiction. Therefore, between every pair of nodes of Ψ_m (x), Ψ_n (x) must have at least one node, and in particular the number of nodes increases with energy.

Transcribed Image Text:

d & (dve v. - v. dite ) = (² Vm dx dx dx 2m 24 (En Em) VmVn.