Magnetic frustration. Consider three spin-1/2 particles arranged on the corners of a triangle and interacting via the Hamiltonian

where J is a positive constant. This interaction favors opposite alignment of neighboring spins (antiferromagnetism, if they are magnetic dipoles), but the triangular arrangement means that this condition cannot be satisfied simultaneously for all three pairs (Figure 4.18). This is known as geometrical “frustration.”
(a) Show that the Hamiltonian can be written in terms of the square of the total spin, S², where S = Σ_i S_i.
(b) Determine the ground state energy, and its degeneracy.
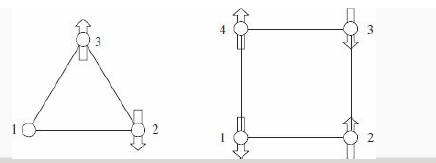
(c) Now consider four spin-1/2 particles arranged on the corners of a square, and interacting with their nearest neighbors:

In this case there is a unique ground state. Show that the Hamiltonian in this case can be written

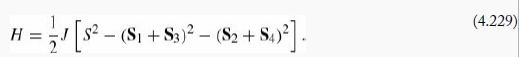
What is the ground state energy?

Figure 4.18

Transcribed Image Text:

H = J (S1 S2 + S2 S3+ S3-S1), (4.227)