Rotations on spin states are given by an expression identical to Equation 6.32, with the spin angular momentum replacing the orbital angular momentum:

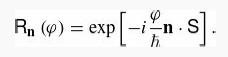In this problem we will consider rotations of a spin-1/2 state.
(a) Show that

where the σi are the Pauli spin matrices and a and b are ordinary vectors. Use the result of Problem 4.29.

(b) Use your result from part (a) to show that

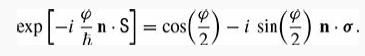
Recall that S = (ћ/2)σ.
(c) Show that your result from part (b) becomes, in the standard basis of spin up and spin down along the z axis, the matrix

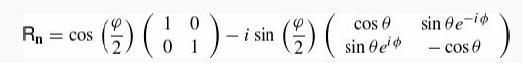
where θ and ϕ are the polar coordinates of the unit vector n that describes the axis of rotation.
(d) Verify that the matrix R_n in part (c) is unitary.
(e) Compute explicitly the matrix S'_x = R⁺S_xR where R is a rotation by an angle φ about the z axis and verify that it returns the expected result.
(f) Construct the matrix for a π rotation about the x axis and verify that it turns an up spin into a down spin.
(g) Find the matrix describing a 2π rotation about the z axis. Why is this answer surprising.

R () = exp[-in.s].