In deriving Equation 6.3 we assumed that our function had a Taylor series. The result holds more generally if we define the exponential of an operator by its spectral decomposition,

rather than its power series. Here I’ve given the operator in Dirac notation; acting on a position-space function (see the discussion on page 123) this means

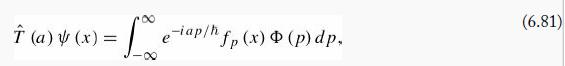
where Φ(p) is the momentum space wave function corresponding to Ψ(x) and fp(x) is defined in Equation 3.32. Show that the operator T̂(a), as given by Equation 6.81, applied to the function

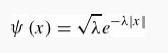
(whose first derivative is undefined at x = 0) gives the correct result.

(a) = [e- = [e-iap/h \p) (p\dp. (6.80)