Consider a time-independent Hamiltonian for a particle moving in one dimension that has stationary states n(x) with

Consider a time-independent Hamiltonian for a particle moving in one dimension that has stationary states Ψn(x) with energies E_n.
(a) Show that the solution to the time-dependent Schrödinger equation can be written

where K(x,x',t), known as the propagator, is

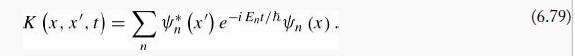
Here |K (x,x',t)|² is the probability for a quantum mechanical particle to travel from position x' to position x in time t.

(b) Find K for a particle of mass m in a simple harmonic oscillator potential of frequency ω. You will need the identity

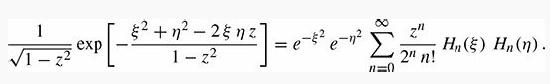
(c) Find if the particle from part (a) is initially in the state

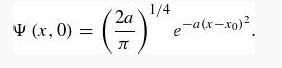
Compare your answer with Problem 2.49.

(d) Find K for a free particle of mass m. In this case the stationary states are continuous, not discrete, and one must make the replacement

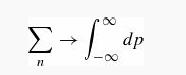
in Equation 6.79.
(e) Find Ψ(x,t) for a free particle that starts out in the state

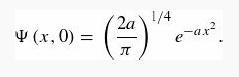
Compare your answer with Problem 2.21.

Transcribed Image Text:

y (x, 1) = Û (1) V (x,0) = [ K (x, x', 1) v (x', 0) dx',