Supersymmetry. Consider the two operators

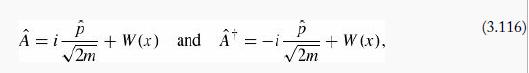
for some function W (x) . These may be multiplied in either order to construct two Hamiltonians:

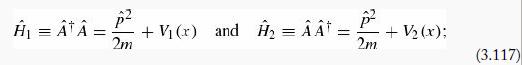
V₁ and V₂ are called supersymmetric partner potentials. The energies and eigenstates of Ĥ₁ and Ĥ₂ are related in interesting ways.
(a) Find the potentials V₁(x) and V₂(x), in terms of the superpotential, w(x).
(b) Show that if Ψ_n(1) is an eigenstate of Ĥ₁ with eigenvalue En⁽¹⁾, then ÂΨ_n(1) is an eigenstate of Ĥ₂ with the same eigenvalue. Similarly, show that if Ψ_n⁽²⁾ (x) is an eigenstate of Ĥ₂ with eigenvalue En⁽²⁾, then ÂΨ_n⁽²⁾is an eigenstate of Ĥ₁ with the same eigenvalue. The two Hamiltonians therefore have essentially identical spectra.
(c) One ordinarily chooses W(x) such that the ground state of Ĥ₁ satisfies

and hence E₀⁽¹⁾ = 0. Use this to find the superpotential W(x), in terms of the ground state wave function, Ψ₀⁽¹⁾ (x). (The fact that  annihilates
Ψ₀⁽¹⁾ means that Ĥ₂ actually has one less eigenstate than Ĥ₁, and is missing the eigenvalue E₀⁽¹⁾.)

(d) Consider the Dirac delta function well,

(the constant term, ma²/2ћ², is included so that E₀⁽¹⁾ = 0). It has a single bound state (Equation 2.132)

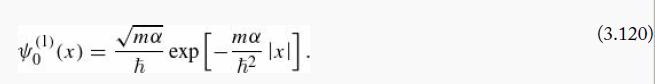
Use the results of parts (a) and (c), and Problem 2.23(b), to determine the superpotential W(x) and the partner potential V₂(x). This partner potential is one that you will likely recognize, and while it has no bound states, the supersymmetry between these two systems explains the fact that their reflection and transmission coefficients are identical (see the last paragraph of Section 2.5.2).

Transcribed Image Text:

Â=i- 2m +W(x) and  =-i- Р /2m + W (x), (3.116)