The Boltzmann equation

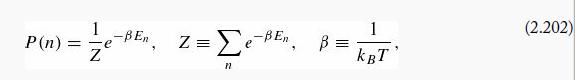
gives the probability of finding a system in the state n (with energy E_n), at temperature T(k_B is Boltzmann's constant). The probability here refers to the random thermal distribution, and has nothing to do with quantum indeterminacy. Quantum mechanics will only enter this problem through quantization of the energies E_n.

(a) Show that the thermal average of the system’s energy can be written as

(b) For a quantum simple harmonic oscillator the index n is the familiar quantum number, and E_n = (n+1/2) ћω. Show that in this case the partition function Z is

You will need to sum a geometric series. Incidentally, for a classical simple harmonic oscillator it can be shown that Z_classical = 2π / (ωβ).

(c) Use your results from parts (a) and (b) to show that for the quantum oscillator

For a classical oscillator the same reasoning would give 

(d) Acrystal consisting of N atoms can be thought of as a collection of 3N oscillators (each atom is attached by springs to its 6 nearest neighbors, along the x, y, and z directions, but those springs are shared by the atoms at the two ends). The heat capacity of the crystal (per atom) will therefore be

Show that (in this model)

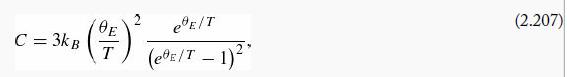
where is the so-called Einstein temperature. The same reasoning using the classical expression for E̅ yields C_classical = 3k_B, independent of temperature.

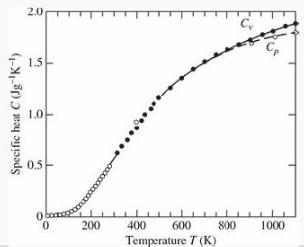
(e) Sketch the graph of C/k_B versus T/θ_E. Your result should look something like the data for diamond in Figure 2.24, and nothing like the classical prediction.

Figure 2.24

Transcribed Image Text:

P (n): = 1 Z e -BEn Z = Σε-βη, β n 1 KBT (2.202)