Legendres differential equation reads where is some (non-negative) real number. (a) Assume a power series solution, and obtain a recursion relation for the constants

Legendre’s differential equation reads

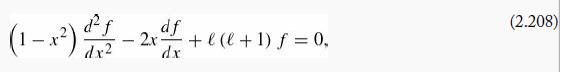
where ℓ is some (non-negative) real number.
(a) Assume a power series solution, and obtain a recursion relation for the constants

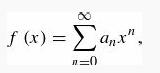(b) Argue that unless the series truncates (which can only happen if ℓ is an integer), the solution will diverge at x = 1.

(c) When ℓ is an integer, the series for one of the two linearly independent solutions (either or depending on whether ℓ is even or odd) will truncate, and those solutions are called Legendre polynomials Pℓ(x).
Find P₃(x), P₃(x), P₃(x), and P₃(x) from the recursion relation. Leave your answer in terms of either a₀ or a₁.

(1-x) 2 - 2x + (+1) = 0, 52 l f df dx (2.208)