Suppose (a) Solve the (time-independent) Schrdinger equation for this potential. by letting z x and y(z)

Suppose

(a) Solve the (time-independent) Schrödinger equation for this potential.
by letting z Ξ αx and y(z)  Ξ (1/√α) Ψ (x) (the √a is just so y (z) is normalized with respect to z when Ψ (x) is normalized with respect to x) . What are the constants a and ε? Actually, we might as well set α → 1  — this amounts to a convenient choice for the unit of length. Find the general solution to this equation (in Mathematica DSolve will do the job). The result is (of course) a linear combination of two (probably unfamiliar) functions. Plot each of them, for (-15 < z < 5). One of them clearly does not go to zero at large z (more precisely, it’s not normalizable), so discard it. The allowed values of ε (and hence of E) are determined by the condition Ψ (0) = 0. Find the ground state є₁ numerically (in Mathematica Find Root will do it), and also the 10th, є₁₀. Obtain the corresponding normalization factors. Plot Ψ₁ (x) and Ψ₁₀ (x), for 0 ≤ z ≤ 16. Just as a check, confirm that Ψ₁ (x) and Ψ₁₀ (x) are orthogonal.
(b) Find (numerically) the uncertainties σ_x and σ_p for these two states, and check that the uncertainty principle is obeyed.
(c) The probability of finding the ball in the neighborhood dx of height x is (of course) The nearest classical analog would be the fraction of time an elastically bouncing ball (with the same energy, E) spends in the neighborhood dx of height x (see Problem 1.11). Show that this is

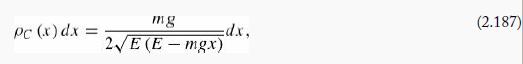or, in our units (with α = 1),

Plot ρQ (x) and ρc (x) for the state Ψ₁₀ (x), on the range 0 ≤ x ≤ 12.5; superimpose the graphs (Show, in Mathematica), and comment on the result.

Transcribed Image Text:

V (x) = mgx, x > 0, x ≤ 0. (2.185)