The Hamiltonian for the Bloch functions (Equation 6.12) can be analyzed with perturbation theory by defining H⁰ and H' such that

In this problem, don’t assume anything about the form of V (x).
(a) Determine the operators H⁰ and H (express them in terms of p̂).
(b) Find E_nq to second order in q. That is, find expressions for A_n, B_n, and C_n (in terms of the E_n0 and matrix elements of p̂ in the “unperturbed” states u_n0)

(c) Show that the constants B_n are all zero. See Problem 2.1(b) to get started. Remember that  u_n0(x) is periodic.
Comment: It is conventional to write C_n = ћ² /2m^*_n where m^*_n is the effective mass of particles in the band since then, as you’ve just shown

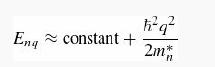
just like the free particle (Equation 2.92) with k → q

Transcribed Image Text:

Ho uno = Eno Uno, (H + H') unq = Eng Ung.