Suppose you want to calculate the expectation value of some observable , in the nth energy eigenstate

Suppose you want to calculate the expectation value of some observable Ω, in the nth energy eigenstate of a system that is perturbed by H':

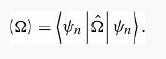
Replacing Ψ_n by its perturbation expansion, Equation 7.5,

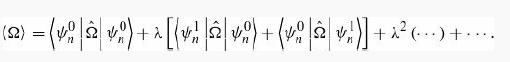
The first-order correction to (Ω) is therefore

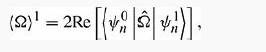
or, using Equation 7.13,

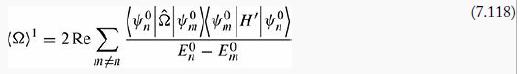
(assuming the unperturbed energies are nondegenerate, or that we are using the “good” basis states).
(a) Suppose Ω = H' (the perturbation itself). What does Equation 7.118 tell us in this case? Explain (carefully) why this is consistent with Equation 7.15.
(b) Consider a particle of charge q (maybe an electron in a hydrogen atom, or a pith ball connected to a spring), that is placed in a weak electric field E_ext pointing in the x direction, so that

The field will induce an electric dipole moment, Pe = qx, in the “atom.” The expectation value of Pe is proportional to the applied field, and the proportionality factor is called the polarizability, α. Show that

Find the polarizability of the ground state of a one-dimensional harmonic oscillator. Compare the classical answer.
(c) Now imagine a particle of mass m in a one-dimensional harmonic oscillator with a small anharmonic perturbation

Find (x) (to first order), in the nth energy eigenstate. Comment: As the temperature increases, high-energy states are populated, and the particles move farther (on average) from their equilibrium positions; that’s why most solids expand with rising temperature.

Transcribed Image Text:

Ω) = 14η ψηλ