The Stoner criterion. The free-electron gas model (Section 5.3.1) ignores the Coulomb repulsion between electrons. Because of the exchange force (Section 5.1.2), Coulomb repulsion has a stronger effect on two electrons with antiparallel spins (which behave in a way like distinguishable particles) than two electrons with parallel spins (whose position wave function must be antisymmetric). As a crude way to take account of Coulomb repulsion, pretend that every pair of electrons with opposite spin carries extra energy U, while electrons with the same spin do not interact at all; this adds ΔE = U N₊N_- to the total energy of the electron gas. As you will show, above a critical value of U, it becomes energetically favorable for the gas to spontaneously magnetize (N₊ ≠ N_-); the material becomes ferromagnetic.

(a) Rewrite ΔE in terms of the density ρ and the magnetization M (Equation 5.74).
(b) Assuming that M/μ_B << ρ, for what minimum value of U is a non-zero magnetization energetically favored? Use the result of Problem 5.32(b).

Equation 5.74

Problem 5.32(b)

Show that for M/μ_B << ρ Ξ (N₊ + N_-)/V (which is to say, |N₊ - N_-| << (N₊ + N_-)), the energy density is

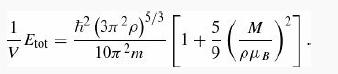
The energy is a minimum for M = 0, so the ground state will have zero magnetization. However, if the gas is placed in a magnetic field (or in the presence of interactions between the particles) it may be energetically favorable for the gas to magnetize. This is explored in Problems 5.33 and 5.34.

Transcribed Image Text:

M = (N₁-N_) V -U Bk = Mk. (5.74)