The harmonic chain consists of N equal masses arranged along a line and connected to their neighbors by identical springs:

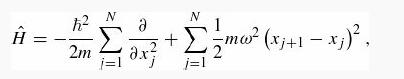
where x_j is the displacement of the jth mass from its equilibrium position. This system (and its extension to two or three dimensions—the harmonic crystal) can be used to model the vibrations of a solid. For simplicity we will use periodic boundary conditions: x_N+1 = x₁, and introduce the ladder operators

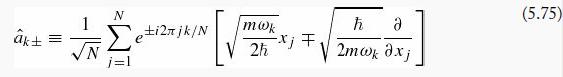
where k = 1, ......, N -1 and the frequencies are given by

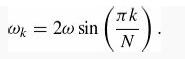
(a) Prove that, for integers k and k' between 1 and N-1,

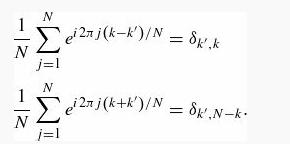
(b) Derive the commutation relations for the ladder operators:

(c) Using Equation 5.75, show that

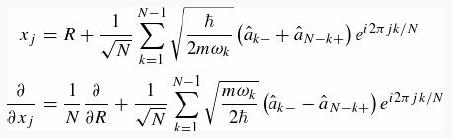
where R = Σ_j xj/N is the center of mass coordinate.
(d) Finally, show that

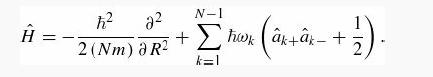
Comment: Written in this form above, the Hamiltonian describes N-1 independent oscillators with frequencies ω_k (as well as a center of mass that moves as a free particle of mass Nm). We can immediately write down the allowed energies:

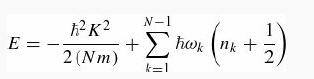
where ћK is the momentum of the center of mass and n_k = 0,1, ... is the energy level of the kth mode of vibration. It is conventional to call the number of phonons in the kth mode. Phonons are the quanta of sound (atomic vibrations), just as photons are the quanta of light. The ladder operators a_k+ and a_k- are called phonon creation and annihilation operators since they increase or decrease the number of phonons in the kth mode.

Transcribed Image Text:

Ĥ = ܕܐ 2 N N Σ + _m«? (x+1=xy)? 1 -mw² 2 p=I