You could derive the spontaneous emission rate (Equation 11.63) without the detour through Einstein’s A and B coefficients if you knew the ground state energy density of the electromagnetic field, ρ₀(ω), for then it would simply be a case of stimulated emission (Equation 11.54). To do this honestly would require quantum electrodynamics, but if you are prepared to believe that the ground state consists of one photon in each classical mode, then the derivation is fairly simple:
(a) To obtain the classical modes, consider an empty cubical box, of side l, with one corner at the origin. Electromagnetic fields (in vacuum) satisfy the classical wave equation

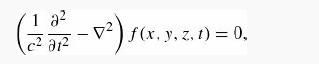
where f stands for any component of E or of B. Show that separation of variables, and the imposition of the boundary condition f = 0 on all six surfaces yields the standing wave patterns

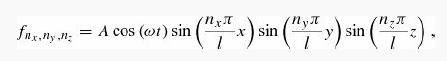
with

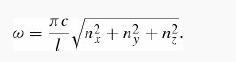
There are two modes for each triplet of positive integers (n_x,n_y,n_z = 1,2,3, ....), corresponding to the two polarization states.
(b) The energy of a photon is E = hv = ћω (Equation 4.92), so the energy in the mode (n_x,n_y,n_z) is

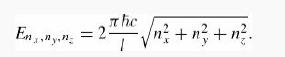
What, then, is the total energy per unit volume in the frequency range dω, if each mode gets one photon? Express your answer in the form

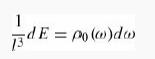
and read off ρ₀(ω). refer to Figure 5.3.
(c) Use your result, together with Equation 11.54, to obtain the spontaneous emission rate. Compare Equation 11.63.

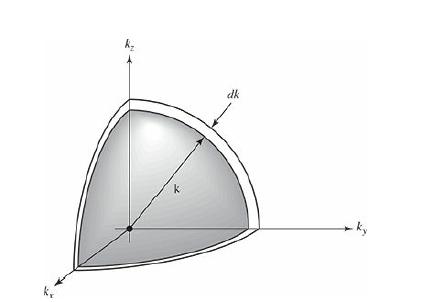
Figure 5.3: One octant of a spherical shell in k-space.

Transcribed Image Text:

a² c² a1² -√²) ₁0 |ƒ (x, y, z, 1) = 0.