Prove Theorem 2.4. That is, prove that [Pleft(bigcup_{i=1}^{n} A_{i}ight) leq sum_{i=1}^{n} Pleft(A_{i}ight)] The most direct approach is
Question:
Prove Theorem 2.4. That is, prove that
\[P\left(\bigcup_{i=1}^{n} A_{i}ight) \leq \sum_{i=1}^{n} P\left(A_{i}ight)\]
The most direct approach is based on mathematical induction using the general addition rule to prove the basis and the induction step. The general addition rule states that for any two events \(A_{1}\) and \(A_{2}, P\left(A_{1} \cup A_{2}ight)=\) \(P\left(A_{1}ight)+P\left(A_{2}ight)-P\left(A_{1} \cap A_{2}ight)\).
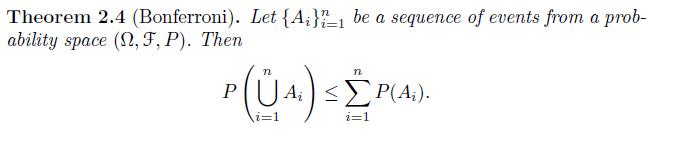
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





