Suppose that \(X\) is a discrete random variable that takes on non-negative integer values and has characteristic function \(\psi(t)=\exp \{\theta[\exp (i t)-1]\}\). Use Theorem 2.29 to find the probability that \(X\) equals \(k\) where \(k \in\{0,1, \ldots\}\).

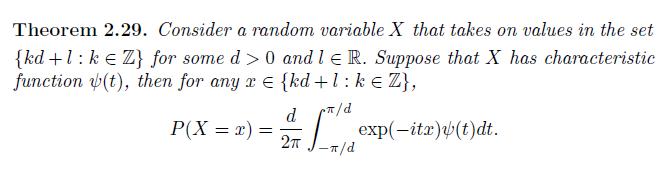
Transcribed Image Text:

Theorem 2.29. Consider a random variable X that takes on values in the set {kd+1kZ} for some d > 0 and 1 R. Suppose that X has characteristic function (t), then for any r = {kd+1: k = Z}, d /d P(X = x)= = exp(-itx)(t)dt. 2T