Suppose that (X_{1}, ldots, X_{n}) are a set of independent and identically distributed random variables from a
Question:
Suppose that \(X_{1}, \ldots, X_{n}\) are a set of independent and identically distributed random variables from a distribution \(F\) that has mean equal to
\(\theta\), variance equal to \(\sigma^{2}\), and cumulant generating function \(c(t)\). Find the form of the polynomials \(p_{1}(x), p_{2}(x)\) and \(p_{3}(x)\) from Theorem 7.5 by considering the form of an expansion for the cumulant generating function of \(n^{1 / 2} \sigma^{-1}\left(\bar{X}_{n}-\thetaight)\) that has an error term equal to \(o\left(n^{-3 / 2}ight)\) as \(n ightarrow \infty\).
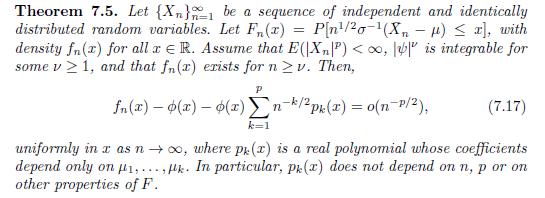
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





