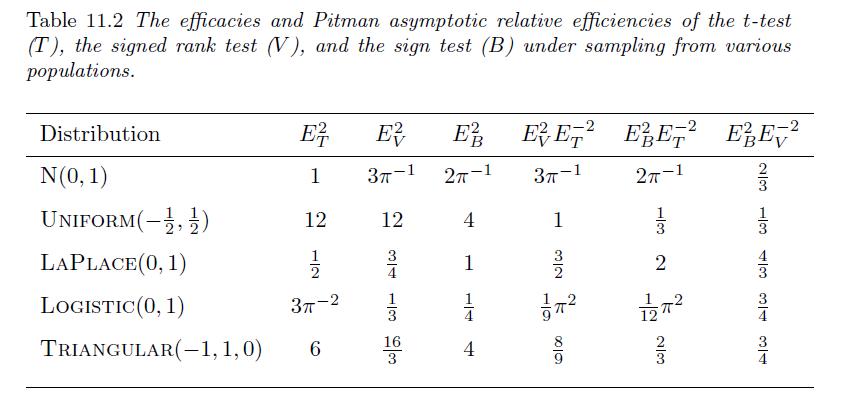
Write a program in \(\mathrm{R}\) that simulates 1000 samples of size \(n\) from a distribution \(F\) with location parameter \(\theta\), where \(n, F\) and \(\theta\) are specified below. For each sample use the sign test, the signed rank test, and the \(t\)-test to test the null hypothesis \(H_{0}: \theta \leq 0\) against the alternative hypothesis \(H_{1}: \theta>0\) at the \(\alpha=0.10\) significance level. Over the 1000 samples keep track of how often the null hypothesis is rejected. Repeat the experiment for \(n=10,25\) and 50 with \(\theta=0.0, \frac{1}{20} \sigma, \frac{2}{20} \sigma, \ldots, \sigma\), where \(\sigma\) is the standard deviation of \(F\). For each sample size and distribution plot the proportion of rejections for each test against the true value of \(\theta\). Discuss how the power of these tests relate to one another in terms of the results of Table 11.2.

a. \(F\) is a \(\mathrm{N}(\theta, 1)\) distribution.

b. \(F\) is a \(\operatorname{Uniform}\left(\theta-\frac{1}{2}, \theta+\frac{1}{2}ight)\) distribution.

c. \(F\) is a \(\operatorname{LaPlace}(\theta, 1)\) distribution.

d. \(F\) is a \(\operatorname{Logistic}(\theta, 1)\) distribution.

e. \(F\) is a Triangular \((-1+\theta, 1+\theta, \theta)\) distribution.

Transcribed Image Text:

Table 11.2 The efficacies and Pitman asymptotic relative efficiencies of the t-test (T), the signed rank test (V), and the sign test (B) under sampling from various populations. Distribution E Ez E EB E N(0,1) 1 3-1 2-1 3-1 2-1 UNIFORM (-) 12 12 4 1 1/3 LAPLACE(0, 1) LOGISTIC(0, 1) TRIANGULAR(-1,1,0) 3-2 6 11 11 16 4 31 13 63 12 3 1 2 2 6100 23 13 43 34 34 12 23