Write a program in (mathrm{R}) that simulates 1000 samples of size 100 from a distribution (F), where
Question:
Write a program in \(\mathrm{R}\) that simulates 1000 samples of size 100 from a distribution \(F\), where \(F\) is specified below. For each sample compute the second and third sample central moments. Use the 1000 simulated values of the two moments to estimate the variance of each sample moment, along with the covariance between the moments. Note that to estimate the covariance it is important to keep the sample central moments from each sample paired with one another. Compare these estimates to what would be expected given the theory in Example 8.14, noting that the assumptions of the example are not met for all of the specified distributions given below.
a. \(\mathrm{N}(0,1)\)
b. \(\operatorname{Cauchy}(0,1)\)
c. \(\mathrm{T}(3)\)
d. Exponential(1)
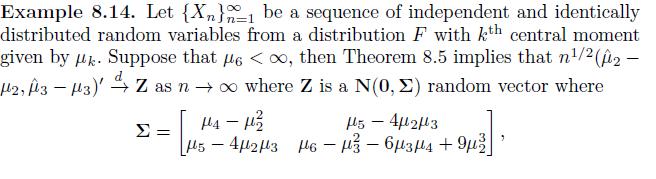
Step by Step Answer:






