A variation on the critical path problem is the task scheduling problem. In this problem, unlike the critical path problem, explicit attention is paid to how many workers are available to do tasks, and the goal is to assign and schedule tasks among workers so that predecessor conditions are satisfied and the project is finished as quickly as possible. Even though a project graph such as those in this section might indicate that a task is ready to be done, there may not be a free worker to do it, so that it might have to wait longer than the critical path algorithm expects. Suppose that there are just two workers available to do the project with tasks listed below. Develop a work schedule for the workers that gets the project done in as little time as possible.

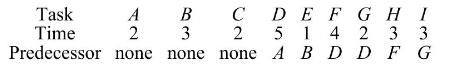
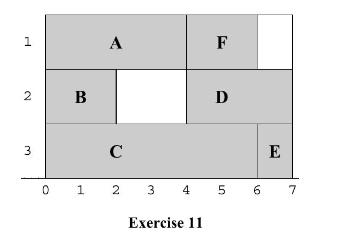
(Hint: A useful device for the scheduling problem is a bar graph that contains one horizontal row for each worker. To schedule tasks consists of placing bars, one per task, of width equal to the time required for the task, end-to-end in the worker rows, obeying predecessor constraints. For instance, in the picture below, there are three workers \(1-3\) and 6 tasks A-F taking \(4,2,6,3,1\), and 2 minutes respectively. The only requirements are that task D must be done after task A, and task E must be done after task C. The work schedule shows worker 1 doing task \(\mathrm{A}\), then beginning task \(\mathrm{F}\) immediately on completion. Worker 2 does task B, then waits until task A is finished, and then does task D. Worker 3 does tasks \(\mathrm{C}\) and \(\mathrm{E}\) in succession. Is this the most efficient schedule?)

Task A B C DEFGHI Time 2 3 2 5 1 4 2 3 3 Predecessor none none none A B D D F G