Consider the following model where a dependent variable \(y\) depends on infinite distributed lags of the two variables \(x\) and \(z\).

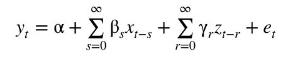
Suppose that both sets of lag weights decline geometrically, but with different parameters \(\lambda_{1}\) and \(\lambda_{2}\). That is, \(\beta_{s}=\lambda_{1}^{s} \beta_{0}\) and \(\gamma_{r}=\lambda_{2}^{r} \gamma_{0}\).

a. Show that the model can be written as

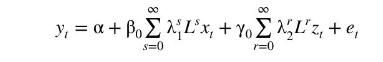
b. Use the result in Exercise 9.15 to show that the equation in (a) can be written as

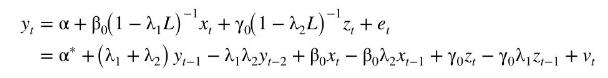
where \(\alpha^{*}=\left(1-\lambda_{1}\right)\left(1-\lambda_{2}\right) \alpha\) and \(v_{t}=e_{t}-\left(\lambda_{1}+\lambda_{2}\right) e_{t-1}+\lambda_{1} \lambda_{2} e_{t-2}\).

c. Using data in the file canada5, with \(y_{t}=I N F_{t}, x_{t}=I N F E X_{t}\), and \(z_{t}=G A P_{t}\), estimate the last equation in part (b) using nonlinear least squares. Report the estimates, their standard errors, and one-tail \(p\)-values for a zero null hypothesis on each parameter (except the constant). Are the estimates significantly different from zero at a \(5 \%\) level?

d. Find estimates of the first three lag weights for both INFEX and GAP.

e. Find estimates of the total multipliers for both INFEX and GAP.

f. Using a \(5 \%\) significance level, test \(H_{0}: \lambda_{1}=\lambda_{2}\) versus \(H_{1}: \lambda_{1} eq \lambda_{2}\). What are the implications for the model if \(H_{0}\) is true?
g. The equation estimated in part (c) can be viewed as a restricted version of the more general \(\operatorname{ARDL}(2,1,1)\) model

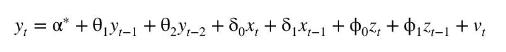
Estimate this unrestricted model and jointly test the validity of the restrictions at a 5\% level. What are the implications for the infinite distributed lags if the restrictions are not true?
h. Test the hypothesis that \(e_{t}\) follows an \(\mathrm{AR}(2)\) process \(e_{t}=\left(\lambda_{1}+\lambda_{2}\right) e_{t-1}-\lambda_{1} \lambda_{2} e_{t-2}+u_{t}\). What are the implications of rejecting this hypothesis?

Data From Exercise 9.15:-

a. Write the \(\mathrm{AR}(1)\) error model \(e_{t}=ho e_{t-1}+v_{t}\) in lag operator notation.

b. Show that

and hence that

Transcribed Image Text:

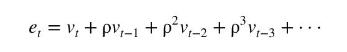
00 y =+Bsxs + V + e + 5=0 1=0