Consider the supply and demand model below: a. Find the reduced-form equations for (p) and (q) as
Question:
Consider the supply and demand model below:
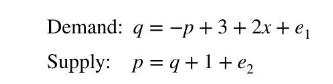
a. Find the reduced-form equations for \(p\) and \(q\) as a function of the exogenous variable \(x\).
b. Now suppose that the demand equation is \(q=-5 p+11+6 x+e_{1}^{*}\). Find the reduced-form equations for \(p\) and \(q\) using this demand equation and the original supply equation.
c. Show that the new demand equation is a mixture of the original supply and demand equations. Specifically, it is three times the original demand equation plus two times the supply equation.
d. If we have \(N\) observations on \(p, q\), and \(x\), can we consistently estimate the supply equation by OLS? Why?
e. If we have \(N\) observations on \(p, q\), and \(x\), can we consistently estimate the reduced-form equations by OLS? Why?
f. Given the economic supply and demand model proposed in the question, is it possible for the mixture equation \(q=-5 p+11+6 x+e_{1}^{*}\) to be a supply curve? Explain.
g. Is the demand equation "identified" using the necessary condition? Is the supply equation "identified" using the necessary condition?
Step by Step Answer:

Principles Of Econometrics
ISBN: 9781118452271
5th Edition
Authors: R Carter Hill, William E Griffiths, Guay C Lim





