Consider a supply and demand model written in its most general implicit form, using capital Greek letters for the unknown parameters and \(E_{i}\) for the random errors:

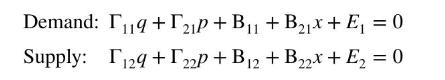
a. Find the reduced-form equation for \(p, p=\pi_{1}+\pi_{2} x+v\). Express \(\pi_{1}\) and \(\pi_{2}\) in terms of parameters \(\Gamma_{i j}\) and \(\mathrm{B}_{i j}\).

b. Suppose we replace the "true" demand equation with an equation that is a mixture of the demand and supply equations, that is, multiply through the demand equation by 3 and the supply equation by 2 and then add the two equations together to obtain

or \(\Gamma_{11}^{\prime} q+\Gamma_{21}^{\prime} p+\mathrm{B}_{11}^{\prime}+\mathrm{B}_{21}^{\prime} x+E_{1}^{\prime}=0\), with ' denoting the new parameters. Using the new demand equation, and the original supply equation, find the reduced-form equation for \(p\), \(p=\pi_{1}^{*}+\pi_{2}^{*} x+v^{*}\). Express \(\pi_{1}^{*}\) and \(\pi_{2}^{*}\) in terms of parameters \(\Gamma_{i j}\) and \(\mathrm{B}_{i j}\). Compare the solution to that in (a).

Transcribed Image Text:

Demand: +21P+B + B21x+ E = 0 Supply: 129+22P+B12+B22x + E = 0