Our aim is to estimate the parameters of the simultaneous equations model

We assume that \(x_{1}\) and \(x_{2}\) are exogenous and uncorrelated with the error terms \(e_{1}\) and \(e_{2}\).

a. Solve the two structural equations for the reduced-form equation for \(y_{2}\), that is, \(y_{2}=\pi_{1} x_{1}+\pi_{2} x_{2}+v_{2}\). Express the reduced-form parameters in terms of the structural parameters and the reduced-form error in terms of the structural parameters and \(e_{1}\) and \(e_{2}\). Show that \(y_{2}\) is correlated with \(e_{1}\).

b. Which equation parameters are consistently estimated using OLS? Explain.

c. Which parameters are "identified," in the simultaneous equations sense? Explain your reasoning.

d. To estimate the parameters of the reduced-form equation for \(y_{2}\) using the method of moments (MOM), which was introduced in Section 10.3, the two moment equations are

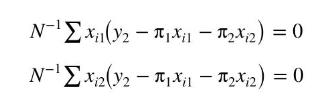
Explain why these two moment conditions are a valid basis for obtaining consistent estimators of the reduced-form parameters.

e. Are the MOM estimators in part (d) the same as the OLS estimators? Form the sum of squared errors function for \(y_{2}=\pi_{1} x_{1}+\pi_{2} x_{2}+v_{2}\) and find the first derivatives. Set these to zero and show that they are equivalent to the two equations in part (d).

f. Using \(\sum x_{i 1}^{2}=1, \sum x_{i 2}^{2}=1, \sum x_{i 1} x_{i 2}=0, \sum x_{i 1} y_{1 i}=2, \sum x_{i 1} y_{2 i}=3, \sum x_{i 2} y_{1 i}=3, \sum x_{i 2} y_{2 i}=4\), and the two moment conditions in part (d) show that the MOM/OLS estimates of \(\pi_{1}\) and \(\pi_{2}\) are \(\hat{\pi}_{1}=3\) and \(\hat{\pi}_{2}=4\).

g. The fitted value \(\hat{y}_{2}=\hat{\pi}_{1} x_{1}+\hat{\pi}_{2} x_{2}\). Explain why we can use the moment condition \(\sum \hat{y}_{i 2}\left(y_{i 1}-\alpha_{1} y_{i 2}\right)=0\) as a valid basis for consistently estimating \(\alpha_{1}\). Obtain the IV estimate of \(\alpha_{1}\).

h. Find the 2SLS estimate of \(\alpha_{1}\) by applying OLS to \(y_{1}=\alpha_{1} \hat{y}_{2}+e_{1}^{*}\). Compare your answer to that in part (g).

Transcribed Image Text:

y2 =2y+B + Bx2 + e Y2