Consider the wage equation, where WAGE is measured in dollars per hour, education and experience are in
Question:
Consider the wage equation,
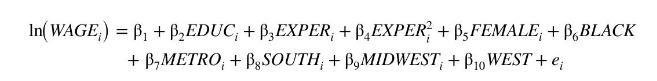
where WAGE is measured in dollars per hour, education and experience are in years, and \(M E T R O=1\) if the person lives in a metropolitan area. Use the data file cps 5 for the exercise.
a. We are curious whether holding education, experience, and METRO equal, there is the same amount of random variation in wages for males and females. Suppose \(\operatorname{var}\left(e_{i} \mid \mathbf{x}_{i}, F E M A L E=0\right)=\sigma_{M}^{2}\) and \(\operatorname{var}\left(e_{i} \mid \mathbf{x}_{i}, F E M A L E=1\right)=\sigma_{F}^{2}\). We specifically wish to test the null hypothesis \(\sigma_{M}^{2}=\sigma_{F}^{2}\) against \(\sigma_{M}^{2} eq \sigma_{F}^{2}\). Carry out a Goldfeld-Quandt test of the null hypothesis at the \(5 \%\) level of significance. Clearly state the value of the test statistic and the rejection region, along with your conclusion.
b. Estimate the model by OLS. Carry out the \(N R^{2}\) test using the right-hand-side variables METRO, FEMALE, BLACK as candidates related to the heteroskedasticity. What do we conclude about heteroskedasticity, at the \(1 \%\) level? Do these results support your conclusions in (a)? Repeat the test using all model explanatory variables as candidates related to the heteroskedasticity.
c. Carry out the White test for heteroskedasticity. What is the \(5 \%\) critical value for the test? What do you conclude?
d. Estimate the model by OLS with White heteroskedasticity robust standard errors. Compared to OLS with conventional standard errors, for which coefficients have interval estimates gotten narrower? For which coefficients have interval estimates gotten wider? Is there an inconsistency in the results?
e. Obtain FGLS estimates using candidate variables METRO and EXPER. How do the interval estimates compare to OLS with robust standard errors, from part (d)?
f. Obtain FGLS estimates with robust standard errors using candidate variables METRO and EXPER. How do the interval estimates compare to those in part (e) and OLS with robust standard errors, from part (d)?
g. If reporting the results of this model in a research paper which one set of estimates would you present? Explain your choice.
Step by Step Answer:

Principles Of Econometrics
ISBN: 9781118452271
5th Edition
Authors: R Carter Hill, William E Griffiths, Guay C Lim





