In this exercise, we explore the relationship between total household expenditures and expenditures on clothing. Use the

Question:

In this exercise, we explore the relationship between total household expenditures and expenditures on clothing. Use the data file malawi_small (malawi has more observations) and observations for which PCLOTHES is positive. We consider three models:

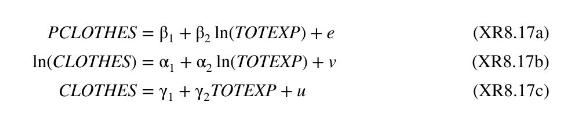
image text in transcribed

a. Plot PCLOTHES versus \(\ln (\) TOTEXP) and include the least squares fitted line. Calculate the point elasticity of clothing expenditures with respect to total expenditures at the means. See Exercise for the elasticity in this model.

b. Calculate CLOTHES \(=\) PCLOTHES \(\times\) TOTEXP. Then plot \(\ln (\) CLOTHES \()\) versus \(\ln (\) TOTEXP \()\) and include the least squares fitted line. Calculate a \(95 \%\) interval estimate of the elasticity of clothing expenditures with respect to total expenditures. Is the elasticity computed in part (a) within this interval?

c. Plot CLOTHES versus TOTEXP and include the least squares fitted line. Calculate a \(95 \%\) interval estimate of the elasticity of clothing expenditures with respect to total expenditures at the means. Is the elasticity computed in part (a) within this interval?

d. Test for the presence of heteroskedasticity in each model in parts (a)-(c). Use the \(1 \%\) level of significance. What are your conclusions? For which specification does heteroskedasticity seem less of an issue?

e. For the models in which heteroskedasticity was significant at the \(1 \%\) level, use OLS with robust standard errors. Calculate a 95\% interval estimate for the elasticity of clothing expenditures with respect to total expenditures at the means. How do the intervals compare to the ones based on conventional standard errors?