Example 11.3 introduces Klein's Model I. a. Do we have an adequate number of IVs to estimate
Question:
Example 11.3 introduces Klein's Model I.
a. Do we have an adequate number of IVs to estimate each equation? Check the necessary condition for the identification of each equation. The necessary condition for identification is that in a system of \(M\) equations at least \(M-1\) variables must be omitted from each equation.
b. An equivalent identification condition is that the number of excluded exogenous variables from the equation must be at least as large as the number of included right-hand side endogenous variables. Check that this condition is satisfied for each equation.
c. Write down in econometric notation the first-stage equation, the reduced form, for \(W_{1 t}\), wages of workers earned in the private sector. Call the parameters \(\pi_{1}, \pi_{2}, \ldots\)
d. Describe the two regression steps of 2SLS estimation of the consumption function. This is not a question about a computer software command.
e. Does following the steps in part (d) produce regression results that are identical to the 2SLS estimates provided by software specifically designed for 2SLS estimation? In particular, will the \(t\)-values be the same?
Data From Example 11.3:-
One of the most widely used econometric examples in the past 50 years is the small, three equation, macroeconomic model of the U.S. economy proposed by Lawrence Klein, the 1980 Nobel Prize winner in Economics. \({ }^{6}\) The model has three equations, which are estimated, and then a number of macroeconomic identities, or definitions, to complete the model. In all, there are eight endogenous variables and eight exogenous variables.
The first equation is a consumption function, in which aggregate consumption in year \(t, C N_{t}\) is related to total wages earned by all workers, \(W_{t}\). Total wages are divided into wages of workers earned in the private sector, \(W_{1 t}\), and wages of workers earned in the public sector, \(W_{2 t}\), so that total wages \(W_{t}=W_{1 t}+W_{2 t}\). Private sector wages \(W_{1 t}\) are endogenous and determined within the structure of the model, as we will see below. Public sector wages \(W_{2 t}\) are exogenous. In addition, consumption expenditures are related to nonwage income (profits) in the current year, \(P_{t}\), which are endogenous, and profits from the previous year, \(P_{t-1}\). Thus, the consumption function is
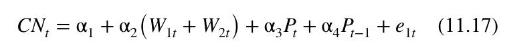
Now refer back to equation (5.44) in Section 5.7.3. There we introduced the term contemporaneously uncorrelated to describe the situation in which an explanatory variable observed at time \(t, x_{t k}\) is uncorrelated with the random error at time \(t, e_{t}\). In the terminology of Chapter 10, the variable \(x_{t k}\) is exogenous if it is contemporaneously uncorrelated with the random error \(e_{t}\). And the variable \(x_{t k}\) is endogenous if it is contemporaneously correlated with the random error \(e_{t}\). In the consumption equation, \(W_{1 t}\) and \(P_{t}\) are endogenous and contemporaneously correlated with the random error \(e_{t}\). On the other hand, wages in the public sector, \(W_{2 t}\), are set by public authority and are assumed exogenous and uncorrelated with the current period random error \(e_{1 t}\). What about profits in the previous year, \(P_{t-1}\) ? They are not correlated with the random error occurring one year later. Lagged endogenous variables are called predetermined variables and are treated just like exogenous variables.
The second equation in the model is the investment equation. Net investment, \(I_{t}\), is specified to be a function of current and lagged profits, \(P_{t}\) and \(P_{t-1}\), as well as the capital stock at the end of the previous year, \(K_{t-1}\). This lagged variable is predetermined and treated as exogenous. The investment equation is
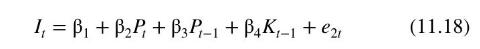
Finally, there is an equation for wages in the private sector, \(W_{1 t}\). Let \(E_{t}=C N_{t}+I_{t}+\left(G_{t}-W_{2 t}\right)\), where \(G_{t}\) is government spending. Consumption and investment are endogenous and government spending and public sector wages are exogenous. The sum, \(E_{t}\), total national product minus public sector wages, is endogenous. Wages are taken to be related to \(E_{t}\) and the predetermined variable \(E_{t-1}\), plus a time trend variable, TIME \(_{t}=\) YEAR \(_{t}-1931\), which is exogenous. The wage equation is

Because there are eight endogenous variables in the entire system there must also be eight equations. Any system of \(M\) endogenous variables must have \(M\) equations to be complete. In addition to the three equations (11.17)-(11.19), which contain five endogenous variables, there are five other definitional equations to complete the system that introduce three further endogenous variables. In total, there are eight exogenous and predetermined variables, which can be used as IVs. The exogenous variables are government spending, \(G_{t}\), public sector wages, \(W_{2 t}\), taxes, \(T X_{t}\), and the time trend variable, TIME . Another exogenous variable is the constant term, the "intercept" variable in each equation, \(X_{1 t} \equiv 1\). The predetermined variables are lagged profits, \(P_{t-1}\), the lagged capital stock, \(K_{t-1}\), and the lagged total national product minus public sector wages, \(E_{t-1}\).
Data From Equation 5.44:-
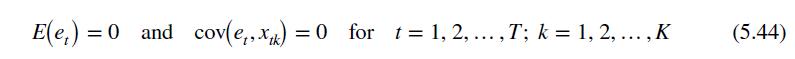
Step by Step Answer:

Principles Of Econometrics
ISBN: 9781118452271
5th Edition
Authors: R Carter Hill, William E Griffiths, Guay C Lim





